ADTs For The Win!

Hello

• Noel Markham
• noel.m@47deg.com
• @noelmarkham

• 47 Degrees
• @47deg

Agenda

• Brief introduction
• Some well-known ADTs
• A brand new collection type

Algebraic Data Types

What is an Algebraic Data Type?

According to Wikipedia:

In computer programming, especially functional programming and type theory, an algebraic data type is a kind of composite type, i.e., a type formed by combining other types.

Not to be confused with abstract data types.

Counting Values

How many different values can these types have:

• Boolean?
• Integer?
• Unit?
• String? List?

Counting Values

What about these types:

• (Boolean, Int)?
• Either[Boolean, Int]?

Tuples are products

Eithers are coproducts

Take a look at Jon Pretty's Talk from flatMap(Oslo) in 2014

Aside: what about function Bool to Int?

Counting Values

(Boolean, Int)

case class Invoice(paid: Boolean, price: Int)

Are they different?

Counting Values

Either[(Boolean, Int), String]

sealed trait DatabaseResponse
case class Invoice(paid: Boolean, price: Int) extends DatabaseResponse
case class ErrorMessage(description: String) extends DatabaseResponse

Is this different to the Either?

Counting Values

• Grouping of types, such as tuples or case classes, are referred to as products
• A choice of type, such as an Either, is referred to as a coproduct or sum type

Other languages, such as Haskell, make this distinction much clearer:

data Suit = Club | Diamond | Heart | Spade

Some common types

Option

sealed abstract class Option[+A]{
  //...
}
final case class Some[+A](value: A) extends Option[A]
  //...
}
case object None extends Option[Nothing] {
  //...
}

Some common types

List

sealed abstract class List[+A] {
  //...
}

final case class ::[B](val head: B, var tl: List[B]) extends List[B] {
  //...				      
}

case object Nil extends List[Nothing] {
  //...				      
}

Some common types

A slightly more interesting example

JSON

We can encode the different types of field allowed in JSON:

• Number
• Boolean
• String
• Array
• JSON object
• Null

Some common types

A slightly more interesting example

JSON

sealed trait Json
case class JsonNumber(d: Double) extends Json
case class JsonBoolean(b: Boolean) extends Json
case class JsonString(s: String) extends Json
case class JsonArray(l: List[Json]) extends Json
case class JsonObject(j: Json) extends Json
case object JsonNull extends Json

Top tip: Take a look at Circe for a nice implementation

What's the value of this?

• Types are good
• A more intuituve and natural encoding of a domain than bare, "primitive" types
• We have a way to encode all possible states, with help from the compiler

• An aside: we can make our Invoice(Boolean, Int) type by replacing the Boolean with an ADT
• Perhaps something like:

sealed trait PaidStatus
case object Paid extends PaidStatus
case object AwaitingPayment extends PaidStatus

What's the value of this?

• We can provide a very safe way to map our ADT on to any other type
• This is usually called folding

Folding

DatabaseResponse => A

There are (at least) a couple of ways we can do this:

• Good old pattern matching
• We can build the functionality into our type

sealed trait DatabaseResponse {
  def fold(fi: (Boolean, Int) => A, fe: String => A): A =
           if(isSuccess) fi(this.paid, this.price) else fe(this.description)
}

Folding

Folding Options

sealed abstract class Option[+A] {
  //...

  final def fold[B](ifEmpty: => B)(f: A => B): B =
    if (isEmpty) ifEmpty else f(this.get)

  //...
}

def map[B](f: A => B): Option[B] = fold(None)(a => Some(f(a)))

def foreach(f: A => Unit): Unit = fold(())(a => f(a))

def get: B = fold(throw new NoSuchElementException("None.get"))(identity)

Folding

Folding JSON

sealed trait Json {

  def fold[A](
    jsonNumber: Double => A,
    jsonBoolean: Boolean => A,
    jsonString: String => A,
    jsonArray: List[Json] => A,
    jsonObject: Json => A,
    jsonNull: => A): A = {
      //...
    }
}

Folding

What's the point?

• We already have pattern matching
• Most folds probably use pattern matching under the hood anyway

Folding

What's the point?

Imagine we add a new class to our DatabaseResponse:

case class PurchaseRequest(item: Item, cost: Int) extends DatabaseResponse

We diligently update our fold:

def fold
    (fi: (Boolean, Int) => A,
     fp: (Item, Int) => A,
     fe: String => A): A = ...

• Top tip: Use folding where possible
• But turn on compiler warnings as errors
• This will help when you non-exhaustively pattern match
  (amongst other things)

Creating our own ADT

Red-Black Trees

From Wikipedia:

A red–black tree is a kind of self-balancing binary search tree. Each node of the binary tree has an extra bit, and that bit is often interpreted as the color (red or black) of the node. These color bits are used to ensure the tree remains approximately balanced during insertions and deletions.

Creating our own ADT

Red-Black Trees

From Purely Functional Data Structures (Chris Okasaki):

• Invariant 1: No red node has a red child
• Invariant 2: Every path from the root to an empty node contains the same number of black nodes

Creating our own ADT

Red-Black Trees

sealed trait Colour[+A]
case class R[A](a: A) extends Colour[A]
case class B[A](a: A) extends Colour[A]

sealed trait Tree[+A]
case object E extends Tree[Nothing]
case class T[A](l: Tree[A], elem: Colour[A], r: Tree[A]) extends Tree[A]

Creating our own ADT

Red-Black Trees

Folding the colour

sealed trait Colour[+A] {
  def fold[X](fr: A => X, fb: A => X): X =
            if(this.isRed) fr(this.a) else fb(this.a)
}

And add a helper to the trait:

def elem: A = fold(identity, identity)

Creating our own ADT

Red-Black Trees

Useful operations

Is a given element in the tree?

def member[A](element: A, tree: Tree[A])(implicit oa: Ordering[A]):Boolean =
 tree match {

  case E => false

  case T(l, c, r) =>
      import oa._
      val e = c.elem
      if (element < e) member(element, l)
      else if (element > e) member(element, r)
      else true
 }

Creating our own ADT

Red-Black Trees

Inserting an element into the tree

def insert[A](element: A, tree: Tree[A])(implicit oa: Ordering[A]): Tree[A] = {

   def ins(t: Tree[A]): Tree[A] =
     t match {

      case E => T(E, R(element), E)

      case T(l, ee, r) =>
        import oa._
        val e = ee.elem
        if (element < e) balance(ins(l), ee, r)
        else if (element > e) balance(l, ee, ins(r))
        else t
   }

   ins(tree)
}

Creating our own ADT

Red-Black Trees

Balancing the tree

We need to turn trees that look like this:

Creating our own ADT

Red-Black Trees

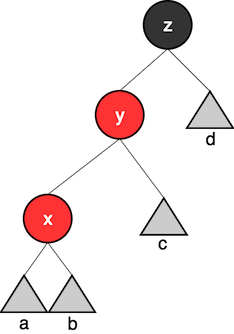
Balancing the tree

Into this:

• Invariant 1: No red node has a red child
• Invariant 2: Every path from the root to an empty node contains the same number of black nodes

Creating our own ADT

Red-Black Trees

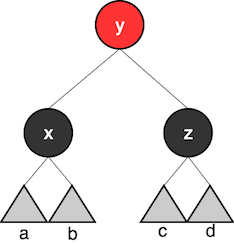
def balance[A](ll: Tree[A], ee: Colour[A], rr: Tree[A]): Tree[A] =
	(ll, ee, rr) match {

    case (T(T(a, R(x), b), R(y), c), B(z), d) =>
				       T(T(a, B(x), b), R(y), T(c, B(z), d))

Creating our own ADT

Red-Black Trees

def balance[A](ll: Tree[A], ee: Colour[A], rr: Tree[A]): Tree[A] =
	(ll, ee, rr) match {

    case (T(T(a, R(x), b), R(y), c), B(z), d) =>
				       T(T(a, B(x), b), R(y), T(c, B(z), d))

   case (T(a, R(x), T(b, R(y), c)), B(z), d) =>
                                       T(T(a, B(x), b), R(y), T(c, B(z), d))

    case (a, B(x), T(T(b, R(y), c), R(z), d)) =>
                                       T(T(a, B(x), b), R(y), T(c, B(z), d))

    case (a, B(x), T(b, R(y), T(c, R(z), d))) =>
	                               T(T(a, B(x), b), R(y), T(c, B(z), d))

    case _ => T(ll, ee, rr)
  }

ADTs for the Win!

• Looked at the algebraic nature of these types
• Explored some common types and implementations
• Used folding
• Created a new collection type using some of these techniques

Thank you